© 2020 All Rights Reserved. Do not distribute or repurpose this work without written permission from the copyright holder(s).

Printed from https://www.damninteresting.com/radical-solutions/

Paris, 29 May 1832. All through the night, a young Frenchman named Évariste Galois stayed awake, quill in hand, frantically scrawling notes and equations across dozens of sheets of paper. He had only been studying mathematics seriously for a few years, but he had proven to be a veritable prodigy. After quickly exhausting the knowledge of his teachers, he’d branched out into his own research, extraordinarily prescient.

By all rights, Galois ought to have been lauded and laurelled by the scientific community for his work. Above all, he should have been recognised and rewarded by France’s prestigious Academy of Sciences. But Galois⁠—at least, by his own reckoning⁠—had received little but dismissal from the mathematics community. Now he sat feverishly scribbling a letter to his best friend, trying to commit as many of his recent ideas to paper as possible. Finally, in the wee hours of the morning, Galois had sketched out most of what he felt able to capture. “You know … that these aren’t the only subjects I’ve explored,” he wrote. “But I don’t have time”. Twenty-year-old Galois fully expected that he was about to be shot to death.

Évariste Galois was born on 25 October 1811 in the town of Bourg-la-Reine, today part of the southern suburbs of Paris. Although his parents ran a well-regarded boarding school of their own, they sent young Évariste to study in Paris shortly before he turned twelve to improve his social opportunities.

Galois’s new school, the Collège royal de Louis-le-Grand was and remains prestigious, but in the early 19th century, it boasted not only an unparalleled list of alumni⁠—among them such luminaries as Voltaire and Charles-Marie de La Condamine⁠—but also a fearsomely draconian atmosphere. Meals were meagre, facilities failing, cold constant, rats regular, and punishments painful, with the students under constant surveillance. The punitive environment⁠—plus homesickness and health issues⁠—took its toll on Galois. In his third year, his grades began to drop, and he earned a reputation as a loner and a troublemaker. One teacher labelled him a “chatterer” who “has, I believe, taken upon himself the task of wearing me out”. That said, Galois’s time at the school would soon lead to two major upheavals in the 14-year-old’s life⁠—one political, the other intellectual.

Galois grew up at the tail-end of France’s revolutionary and Napoleonic years, which had infused the country’s intellectual bloodstream with liberal ideas. Despite the restored monarchy’s attempts to crack down on this unseemly radicalism, the school had developed a liberal reputation. A new school principal, Nicolas Berthot, thought this merited a course correction, and set about inaugurating new rules harkening back to the school’s harsh old Jesuit roots. In response, students undertook a campaign of nonviolent resistance⁠—when asked to sing hymns, speak in class, or toast the King at meals, they remained mute. Berthot, apparently not one for half measures, simply expelled the students⁠—over 100 of them. While Galois was not directly involved, he was appalled by Berthot’s peremptory reaction. It was in this atmosphere of injustice and oppression that young Galois began his shift from mere liberal-minded student to full-blown anti-authoritarian.

In contrast, Galois’s academic upheaval was due to a happy convergence between an academic restructuring and his own academic failure. With his grades plummeting, he was forced to repeat his entire third year. This cannot have been welcome news, but there was an unexpected upside. The third-year curriculum had just been changed, and would now introduce students to arithmetic and geometry alongside their continued study of the classics. Galois was about to meet mathematics. Few blind dates have gone so well.

Instantly sparked, the 15-year-old devoured entire textbooks on algebra, calculus, and geometry. Galois’s other classes, already somewhat neglected, fell off his radar almost entirely. Faculty soon abandoned all hope of getting any other subject into his brain.

Galois leapt straight into a heavily intuitive, original approach to tackling big unanswered questions. His concerned teachers suggested that he outline his problem-solving more methodically, or at least follow the basics of showing his work, but he was not interested in such elementary claptrap. Within mere months, he had outgrown his coursework and reached the extremities of contemporary mathematical knowledge.

Fully aware of his own preternatural talent, Galois set his sights on attending the École polytechnique⁠—France’s foremost technical school⁠—as soon as possible. As he was nearing 16, the minimum age of admission, he registered for the entrance exam immediately. Nearly as immediately, he failed. Still, failing the entrance exam was nothing to be ashamed of. Many students went into their first attempts seeking only to get a sense of how the exam worked⁠—which made sense, as it was a fast-paced verbal interrogation at a blackboard. Just one in three examinees passed on their first try. Though Galois’s failure forced him to remain at Louis-le-Grand, he could at least console himself that this was only a temporary setback.

A further consolation appeared in the form of an enthusiastic new mathematics teacher who grasped the scope of Galois’s ideas and quickly became his mentor. Under this mentor’s guidance, in April 1829, 17-year-old Galois published a short paper on repeating fractions in a respected scholarly journal. Impressive though this was, for Galois this was only a side-project, dwarfed by breakthroughs he was making in the area of polynomial equations. This was a big deal. Mathematicians had collectively hit a wall with polynomials late in the 18th century, and Galois was about to suggest a way over.

For people who remember algebra classes, the most familiar type of polynomial is the quadratic equation, which can be useful in calculating areas, solving some accounting tasks, and addressing some physics problems. It is generally written as:

“X” is the single unknown value to solve for. There are multiple ways of figuring out the possible value(s) for x, but one reliable way is by taking a, b, and c and plugging them into a formula that was discovered by Spanish mathematician Abraham bar Hiyya Ha-Nasi around the year 1100 AD. It is fittingly known as the quadratic formula:

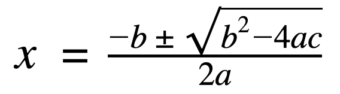
What makes a quadratic equation ‘quadratic’ is that x is squared, or to the power of 2. So a quadratic equation is said to have a degree of 2. An equation where x is to the power of 3 (but nothing more) has a degree of 3, and these are called cubic equations, which look like this:

The quadratic formula doesn’t help with cubic equations, but a working cubic formula was discovered sequentially by three Italian mathematicians in the 16th century. A student of one of theirs went one further, literally, managing to find an enormously complicated general formula for quartic equations⁠—those of degree 4.

The outstanding question Galois wished to tackle was: Is there a formula to solve quintic equations, i.e. those of degree 5? Prominent mathematicians of the day suspected that a general solution for quintic equations simply did not exist. However, a mere failure to find such a formula was not evidence. Italian mathematician Paolo Ruffini came close to proving that no such general solution existed for 5th-degree equations, which he published in a paper in 1799.

Picking up more or less where Ruffini left off, 17-year-old Galois set out to prove that no general formula existed for quintic equations. More broadly, Galois took an interest in an overarching question: what determined whether or not a general formula exists for a given degree?

Galois’s approach to untangling the matter was stunningly original. He tied equations to several major new conceptual frames. He identified groups: sets of entities linked by a specific set of certain properties. Then permutations: all the different ways of ordering the members of a set. And symmetries: ways in which entities look like other parts of themselves. There was so much uncharted territory here that Galois found himself inventing a brand-new approach to algebra. The system he devised for describing the subtle internal characteristics of groups⁠—group theory⁠—was almost unprecedented, but so versatile that it could capture the behaviour of not only numbers, but all sorts of grouped items and ways in which their components showed self-similarity. When it came to polynomials, Galois’s major insight was that solvability of a given equation ultimately had far less to do with the equation’s degree, and far more to do with its internal properties related to symmetry. Astrophysicist and popular-mathematics author Mario Livio offers this analogy:

“Classifying equations by their degree is analogous to grouping the wooden building blocks in a toy box according to their sizes. Galois’s classification by symmetry properties is equivalent to the realization that the shape of the blocks⁠—round, square, or triangular⁠—was a more important characteristic.”

Using his own new group theory to break a complicated polynomial equation into smaller pieces and test those for solvability, Galois showed definitively that quintic equations, considered as a set, would not resolve this way. His results gave mathematics a way of determining whether a particular polynomial can be solved through a formula. All polynomials of degrees 2, 3, and 4 qualified. Starting at degree 5, however, some did and others did not⁠—and thus there was no way a general solution could apply to all of them.

Galois’s mentor Louis Richard, for one, was well-aware that the boy’s ideas were visionary. Richard decided to help his brilliant protégé submit two papers to the Academy of Sciences in the spring of 1829. Getting the Academy’s attention was an essential step for any aspiring mathematician in France at the time. It was the most prestigious scientific organisation in the country, and having a paper accepted there would be a spectacular feather in Galois’s cap. It wouldn’t hurt when it came to his second attempt at being admitted to the Polytechnique, either.

Only members of the Academy could present new findings to the august body, so Galois needed to find a willing sponsor to present papers on his behalf. Richard reached out to the revered Augustin-Louis Cauchy, likely because 15 years earlier, Cauchy had published two papers on general theories of permutations. Cauchy, one of the most prolific mathematicians in history, rarely had time to read and endorse other people’s work⁠—but in this case, against the odds, he agreed. In May and June 1829, he presented a pair of complementary papers by Galois to the Academy of Sciences, and made plans to present a third in January 1830.

But the thrill was about to be brutally crushed. A new priest had been assigned to Galois’s hometown of Bourg-la-Reine, one who immediately clashed with its liberal and warmhearted mayor⁠—who happened to be Galois’s father, Nicolas-Gabriel Galois. Determined to save the souls of his parish from the insidious influences of broad-mindedness and insufficient monarchism, the priest devised a plan to undermine the elder Galois and force him out of office. The well-liked Nicolas-Gabriel had a fondness for playful writing at times – delighting the townsfolk with short coupled rhymes. Taking note of this idiosyncracy, the priest began to author his own rhyming couplets in the mayor’s characteristic style, making them mean-spirited rather than playful, and signing them with Nicolas-Gabriel’s name. The slanderous counterfeits spread. Ultimately, the plot proved even more successful than the priest had hoped. In July 1829, devastated by the impersonation and by the loss of his good name, Nicolas-Gabriel Galois took his own life. He had been the mayor of the town for 15 years.

The truth quickly emerged. Astoundingly, the priest attempted to take part in the funeral ceremony⁠—only to find himself fleeing a mob of furious townspeople and volleys of stones. Galois witnessed the entire scene, and his grief and rage can only be imagined. He had already had reason to resent and oppose his country’s religious right wing: the political had now become intensely personal.

And then, with spectacularly bad timing, the next round of entrance exams for the École polytechnique was upon him. Galois⁠—short-tempered at the best of times, labouring under the emotional toll of his father’s death, convinced of his own genius, already bitter at the perceived injustice of having been rejected the first time around⁠—was in no state to deal with a second high-stakes examination at a blackboard. He was never at his best explaining ideas verbally in the first place, and he had spent the year working on original research rather than preparing for the examination. On top of that, Galois’s examiner was a man known for asking extremely simple questions⁠—not to test candidates’ knowledge, but to gauge their reaction to being asked them. Faced with an examiner who struck him as blitheringly ignorant, Galois did not do well. Unverified legend has long claimed that the exam came to an end when the candidate flung the eraser at the examiner’s face.

Whether it was his mathematics or his temper that sunk him, Galois was again denied admission to the Polytechnique. He turned his attention to a backup option: the École préparatoire (Preparatory School), whose main job was training teachers. It had its own set of entrance exams⁠—across a range of subjects, including several that were not mathematics. Although the application deadline for the school had passed, Galois wrote a letter to the administration asking them to let him apply anyway. His letter suggests that recent events had not compromised his cockiness. The examiners allowed him to proceed, but the science adjudicator in particular was less than impressed, commenting dryly that Galois “knows absolutely nothing”:

“I was told this student had an aptitude for Mathematics; this surprises me greatly, as based on his examination, I think he possesses very little intelligence, or, at least, it’s so well hidden that I was unable to discover it[.]”

Nevertheless, Galois’s scores for mathematics were high enough⁠—and his answers, for a change, expressed clearly enough⁠—that he was admitted to the École préparatoire in November 1829.

Galois had a way forward. However, his fledgling mathematics career ran into turbulence shortly after takeoff, due to the untimely death of a Norwegian mathematician named Niels Henrik Abel. Amiable but hapless, Abel had been unsuccessfully clamoring for attention from French mathematicians for years. He had even travelled to Paris to seek recognition, and sent one of his own papers to Augustin-Louis Cauchy. Alas, Cauchy had failed to get around to reading it. Even Abel’s defeated letter to Cauchy several years later, requesting the return of his manuscript, went unacknowledged. Then, only 26 years old, Abel succumbed to tuberculosis.

When news of Abel’s death reached the Academy in June 1829, Cauchy scrambled to defend himself⁠—awkwardly and unconvincingly⁠—for having neglected the young Norwegian. He rushed to read Abel’s three-year-old manuscript and present it to the Academy, just a few weeks after his second presentation on Galois’s work. It was immediately apparent that Abel had reached many of the same conclusions as Galois, and done so earlier⁠—publishing a proof that there could be no general formula for polynomials of any individual degree of 5 or above. That autumn, the Bulletin de Férussac published both an obituary of Abel and a detailed analysis of one of his earlier papers. For those in the know, this underscored the fact that while Galois had made some phenomenal breakthroughs, Abel had reached some of the same insights first. Their methods were entirely distinct, but when it came to the conclusions, Galois⁠—nine years younger⁠—had been provably pre-empted. Unsurprisingly, Cauchy’s planned third presentation of Galois’s research did not go ahead as planned in 1830⁠—though, as science historian René Taton points out, the normally irascible Galois did not complain about this, which suggests that he voluntarily withdrew his work given the unintended overlap with Abel’s findings.

That said, Galois could still salvage the considerable original components of his own work. Abel had not scooped him on group theory. While keeping up with his regular schoolwork, Galois compiled his research into a manuscript and submitted it at the end of February 1830 to the Academy’s inaugural Grand Prize in mathematics. Despite a few setbacks, Galois was carving himself a respectable place in the mathematical world. If he were to win the Grand Prize, it would cement his status as a leading light of his generation.

On 28 June 1830, the results of the Grand Prize were announced, and Galois’s name was nowhere to be seen. The jury chose to award the prize to two mathematicians for their separate work on elliptic functions. One was the German Carl Gustav Jacob Jacobi; the other, posthumously, was Abel. A clause in the contest rules specified that the jury could award the prize to any paper published in the previous year, not just official entries; the Academy thus made amends to the memory of the young man it had ignored in life.

Another young man, however, was available to feel disregarded in Abel’s place. Galois could not possibly have objected to the winners on mathematical grounds; he strongly identified with Abel, and Jacobi appears to have been one of the few other mathematicians he respected. What was galling for Galois was that his manuscript was not even listed as an official contest entry. Indeed, when he asked to have his paper returned, it could not be found. This turned out to be simple bad luck. The Permanent Secretary of the Academy, Joseph Fourier, had served on the jury for the Grand Prize, and had taken Galois’s manuscript home with him to read. Unfortunately, he died in mid-May; Galois’s manuscript was lost somewhere in the shuffle of his papers, and it never resurfaced.

Galois already had a sizable chip on one shoulder, and was fast developing one on the other as well. He was increasingly convinced that the Academy was deliberately shunning him. Perhaps, he thought, they were too incompetent to understand his dramatically forward-thinking mathematical ideas and too stodgy to approve of his dramatically forward-thinking political convictions. Galois’s resentment can only have been compounded when, in late July 1830, he took an exam on differential and integral calculus and placed only fourth out of eight students⁠—a shockingly low rank for someone who was having papers published in the same journal as Cauchy. On top of it all, he was still irritated at having twice been denied the chance to study at the Polytechnique, both for the quality of its mathematics instruction and for its opportunities in the way of anti-monarchist political activism. The second of these was about to be on full display as the tectonic plates of French politics shifted in the summer of 1830.

King Charles X, to put it mildly, was extremely conservative. The ministers he chose were even more so. All of them remained traumatised by the French Revolution of 1789, which had resulted in the mass decapitation of their peers⁠—including more than a few members of Charles’s family. As a result, they were dedicated to doing away with those ridiculous ideas of liberty, equality, and fraternity that the revolution had propagated.

When the results of an election in the summer of 1830 favoured the liberal left, the government’s ossified leaders retaliated with a particularly boneheaded decision. A series of decrees dissolved the newly elected legislature before it had even met, reduced the assembly’s size by 170 seats, drastically curtailed voting rights in favour of the wealthy, censored opposition publications, and called for a do-over election in September. The government must have expected that the liberals would be unhappy, but as the prime minister reported that he received regular visitations from the Virgin Mary and she had told him everything would be fine, they went ahead anyway. What they didn’t take into account was that essentially abolishing the printing industry would also make the typographers unhappy. With their livelihoods gone, they spilled into the streets, quickly followed by their working-class peers, and then the furious middle class.

Riots became the lightning-speed July Revolution, which quickly became mythologised as the Trois Glorieuses, the “Three Glorious Days”, where all classes had united to throw out a tyrannous regime. Members of the democratically organised National Guard⁠—which had been founded during the Revolution but that Charles had abolished⁠—pulled out their old uniforms from the cupboard and spontaneously reformed the militia. They came to be known as the heroes of the hour⁠—along with the students of the Polytechnique, who also jumped into the fray.

Their counterparts at the École préparatoire, on the other hand, were shut out. Or, more precisely, shut in. As the battle raged on the streets of Paris, the school’s administrators locked the doors to keep their students from taking part. The school’s new principal, Joseph-Daniel Guigniault, twice threatened to call in the military to keep order among his pupils. (This might not have accomplished anything. The royalist army was a bit preoccupied, trying to control the streets while upper-storey inhabitants of buildings showered them with furniture, including the occasional piano.) Guigniault made matters worse by uttering condescending comments about the revolutionaries. As it was, he could at least claim that he kept his students safe. The only one of them who seems to have been at any risk of injury during the Trois Glorieuses was Galois, who by most reports was so eager to get involved with the rioting that he tried to climb over the schoolyard wall.

His participation was unnecessary. Charles X faced the facts and went off into exile, while France proclaimed a new constitutional monarchy under a new king, Louis-Philippe. The National Guard became a key part of the imagery surrounding the change, their blue-white-red uniforms matching the newly restored tricolour flag flapping everywhere.

The new regime, however, did not please everyone: it was a compromise that did not go far enough for the left and was anathema to the right. Paris, which set the tone for the whole country, remained a cramped medieval city with an underpaid, underfed working class. There were ongoing flare-ups of both rioting and disease. For Galois, the revolution also meant the loss of his best source of support at the Academy of Sciences: Cauchy, who was a right-wing Catholic and diehard supporter of the old monarchy, had left the country rather than take the required oath of loyalty to the new king.

Galois’s own path, naturally, was diametrically opposed. He joined the newly founded Société des amis du peuple, a republican group so radical that it was banned altogether in October 1830, after which it became a (theoretically) secret society. While the Polytechnique was being laurelled for its active liberalism, Galois was stuck behind locked doors with its despised principal Guigniault⁠—his best chance at fighting the Establishment being stifled by the Establishment. To Galois, the principal’s behaviour was infuriatingly hypocritical. At first, Guigniault had mocked and dismissed the revolutionaries⁠—only to drape himself ostentatiously in the tricolour of those same revolutionaries at the battle’s end. Guigniault also made the empty gesture of changing the name of the school itself back to its Napoleon-era name of École normale, while at the same time continuing to insist that “good students should not be interested in politics”.

Galois exchanged an increasingly testy series of letters with school administrators, criticising Guigniault’s response to the riots and revolution. When Galois published an “anonymous” letter in a prominent education-focused journal, spilling the matter into the press and thus the public, Guigniault simply expelled him.

With school off the table, nothing prevented Galois from getting in on the glory of the National Guard. The young mathematician enlisted in one of the Guard’s artillery batteries, one known to be a hotbed of republican sentiment. A good chance lay ahead for the republicans to demonstrate their continued displeasure with current affairs. Several of Charles X’s ministers were on trial, and the consensus on the left was that anything less than death sentences would be tantamount to acquittal⁠—and grounds for another uprising.

Wearing a newly purchased uniform, Galois would have been among the artillerymen stationed at the Louvre on 21 December 1830 when the sentences were announced. The ministers were sentenced to life in prison rather than death. The situation was precarious for days, and several members of the artillery were arrested for seditious behaviour. King Louis-Philippe, no fool, realised that leaving a bunch of radical republicans in charge of cannons might not be the wisest course. On 31 December, he dissolved the National Guard’s artillery units, outlawing the wearing of their uniforms. Galois’s military career had lasted, at most, three weeks.

Untethered from all institutions, Galois floundered, but the Academy of Sciences extended an olive branch. One of its most respected mathematicians, Siméon Denis Poisson⁠—who had shared journal space with both Galois and Cauchy just a few months earlier⁠—requested that Galois send them a new paper. Galois wrote a new manuscript⁠—probably a re-creation of his lost submission to the Grand Prize⁠—and submitted it on 17 January 1831. After two months passed with no word, Galois followed up with a snide letter to the President of the Academy, suggesting there was something fishy in Poisson’s delay. Pointedly rehashing his experience, Galois topped it off with a direct accusation of ulterior motives:

“…the examining committee decided a priori that I could not have resolved this problem, firstly because my name was Galois, and moreover because I was a student. And the committee misplaced my paper. And I was told that my paper was misplaced. This lesson should have sufficed me […] to this day, my research has met more or less the same fate […] Will the analogy be pursued to the end? Please […] invite Messrs. Lacroix and Poisson to declare whether they have misplaced my paper, or whether they intend to report on it to the Academy.”

Needless to say, this was not a good strategy for building a career. Other mathematicians were left shaking their heads at Galois’s behaviour. Rumours flew that he was losing his mind.

On 16 April 1831, nineteen of Galois’s fellow republicans were acquitted of sedition charges. Overjoyed, their allies carried them home in triumph, and quickly decided to hold a celebratory banquet in their honour. There was no right to free association in France at the time, but even the most dictatorial regimes knew better than to get between the French and a good meal. A banquet was therefore one of very few legal ways of gathering a large group of like-minded people to exchange ideas (or to collectively decide to defenestrate a bust of the king, or both). The venue was a restaurant, but not one known for its cuisine. Rather, it was the largest space in Paris that a group could book easily. A year earlier, it had hosted a liberal banquet that had laid the groundwork for the end of Charles X’s rule. Now Galois looked forward to a similar event⁠—and in preparation, he visited a local knife-maker and very eagerly ordered a ‘folding dagger’.

One of the other revolutionaries in attendance at the banquet was Alexandre Dumas. The future creator of the Three Musketeers and the Count of Monte Cristo, Dumas was already a renowned playwright; only a week earlier, one of his plays had become the theatrical sensation of the year. He had also been an artilleryman in the same National Guard battery as Galois and many of the nineteen acquitted republicans. Recalling the event much later in his Memoirs, Dumas wrote that “it would have been difficult to find two hundred people more hostile to the government in all of Paris”. Even so, Galois eventually managed to find a way to stand out. As the number of emptied champagne bottles grew and the banqueters began to forego their promise not to make any unapproved toasts, Dumas suddenly became aware that

“[a]n extremely animated scene was taking place fifteen or twenty places down from me. A young man, holding his raised glass and an open dagger in the same hand, was striving to make himself heard. It was Évariste Galois, […] one of the most ardent republicans.”

Ardent and, it must be said, drunk. Galois later admitted to a friend that if he’d been sober, he would never have behaved as he did. Dumas could not hear over the immediate roar of the crowd, but he did work out that the words “Louis-Philippe” had been uttered, that Galois’s open dagger was unambiguous, and that there were limits to his own radicalism. Catching each other’s eye, Dumas and his neighbour hopped out a window and skedaddled⁠—which, from a banquet on the ground floor, was admittedly easier than it might have been.

What Galois had done was to openly call for regicide⁠—a crime so unthinkable that the criminal code classified it as being as unnatural as parricide. Dumas knew well that plays could be banned simply for alluding to it. This action was too radical even for the radicals: republicans did not want their movement reminding the nation of the constant guillotining that had marked the 1789 Revolution. But Galois’s fiery outburst was soon all over the newspapers, causing considerable embarrassment. The morning after the banquet, Galois was arrested at his mother’s house.

Galois’s supporters latched onto the fact that the threat had technically been conditional⁠—“To Louis-Philippe, should he betray [his oath to uphold the constitution]”⁠—with the crowd’s noise burying the second half. Astonishingly, at his own trial on 15 June 1831, Galois did not take advantage of this escape rope. Instead, he doubled down in every possible way. Not only did he not blame drunkenness, he insisted that he had intended what he’d said, conditionals be damned. In open court, with a gobsmacked audience looking on, Galois confirmed that it had been an assassination threat, that he had not just been expressing his personal opinion, and that he was attempting to goad others into making attempts on the king’s life. Indeed, Galois went on, in his opinion Louis-Philippe probably already had betrayed his oath. Around this point, the judge cut the interrogation short⁠—either to keep a lid on Galois’s outrageous sentiments, or simply to stop him from digging himself even more deeply into a hole.

Surprisingly, Galois was acquitted. Dumas’s explanation was that the jurors either agreed with Galois, or simply thought he was beyond sanity. Most other sources agree that the judge and jury took pity on him because he was so young⁠—still only 19.

Against the odds, Galois had slipped out of the political noose. Not only that, but the publicity dislodged the apparent impasse at the Academy of Sciences. On the day his trial started, the newspaper Le Globe published a lengthy letter detailing Galois’s experiences with the Academy. Specifically, the publication argued that Poisson⁠—who had requested the new paper from Galois in the first place⁠—had really dropped the ball. Perhaps encouraged to hurry, Poisson and his co-referee submitted their report a few weeks after Galois’s acquittal, on 4 July 1831, then presented it publicly to the Academy a week later.

A months-long wait for a response to a manuscript was not actually anything unusual. The Academy was swamped with submissions. Mathematical historian Caroline Ehrhardt reports that two-thirds of the papers submitted to the Academy never received a report at all⁠—and of those that did, few got more than a few terse sentences. Galois’s complaint of neglect in March was baseless. Fortunately, the Academy did not dismiss him out-of-hand for his impudence⁠—which is just as well, for this manuscript contained what astrophysicist/author Mario Livio later called “one of the most imaginative breakthroughs in the history of algebra”⁠—the core of his invention of group theory.

To their credit, the reviewers produced a lengthy, thorough, and detailed report on Galois’s manuscript. It was clear that they saw and appreciated the links between Galois’s ideas and Abel’s. But their evaluation was not what Galois had hoped for: overall, Poisson and Lacroix confessed that they were baffled. The math itself was not the problem; rather, they were not always able to follow the argumentation.

“[…] we have made every effort to understand Mr. Galois’s demonstration. His reasoning is neither clear enough not developed enough for us to have been able to judge its exactness […] The author announces that this proposition […] is part of a general theory liable of many other applications. It is often the case that the different parts of a theory, by mutually illuminating one another, are easier to grasp when taken together rather than in isolation. We can therefore wait for the author to have published his work in its entirety before coming to a definitive opinion […]”

Several contextual factors worked against Galois. He still did not have training in the conventions of writing out mathematical discoveries⁠—a skill he could have picked up at the Polytechnique. Added to this, his work was pure mathematics; this would have resonated with the absent Cauchy, but for the other members of the Academy at the time, what was important was applied mathematics. Plus, algebra was still thought of as a tool rather than a subfield of mathematics in and of itself; Poisson and Lacroix would have been judging Galois’s manuscript through the lens of mathematical analysis⁠—what we now call differential calculus⁠—and looking for its practical potential. Galois’s ideas likely struck them as a pointless excursion into terra incognita. With the benefit of hindsight, Mario Livio slams the reviewers for reacting so lukewarmly to Galois’s manuscript. However, in modern academic parlance, the referees’ report is much more “revise and resubmit” than it is an outright rejection. More than one modern mathematician has admitted they would likely have made the same decision in response to the manuscript as it was.

None of this counted for Galois. Furious, he became convinced once and for all that the Academy was out to get him. And as usual, mathematical disappointment dovetailed with political trouble. Only days later, on 14 July 1831, the police set out very early for Galois’s home. Knowing him to be a troublemaker, they were hoping to nab him in a pre-emptive roundup of republican rowdies known to have plans for commemorating the fall of the Bastille. No Évariste Galois was found⁠—because he had already left home that morning. The police eventually caught up with him and his friend Ernest Duchâtelet. The young men were going to an illegal march, with Galois illegally wearing his National Guard uniform⁠—not to mention carrying a rifle, a couple of pistols, and a dagger. Placed under arrest, the pair complied calmly enough that the officers didn’t think to confiscate their prisoners’ rifles until they were halfway to the police station.

Galois was thrown in jail to await trial, but his stay in Sainte-Pélagie prison got off to an eventful start. As the anniversary of the July Revolution approached, the republican prisoners got more and more excited. On 28 July 1831, they happily spent the day yelling anti-royalist slogans, insulting passers-by, and throwing things out of windows. Towards evening, a loaf of bread hit a woman on the head so hard that she was left bruised and bleeding (a testament to the sort of food the inmates were given). Half an hour later, one of Galois’s cellmates began to caterwaul La Marseillaise as he undressed for bed in front of the window. Outside, an exasperated local citizen sick of the ruckus let off a round of buckshot that hit the man clear in the face. Inside, panic erupted. The guards on the scene managed to regain control only by throwing three of the inmates⁠—including both Galois and Monsieur La Marseillaise⁠—into the dungeon. This action itself nearly caused a riot, and rumours flew that the shot had been fired by a prison employee at the governor’s order.

Galois was only in the dungeon for three days, but it was three months before he came to trial. This time around, Galois backed down and feebly claimed that he hadn’t realised that wearing his uniform was illegal. The judge was unconvinced. Probably feeling that Galois’s previous acquittal had failed to teach him a much-needed lesson, he sentenced the young man to a further six months in jail. This sentence was disproportionately long, especially considering that Duchâtelet⁠—who had sketched a guillotine on his cell wall and added verses that threatened Louis-Philippe⁠—would have to do only three.

Imprisonment did not suit Galois. Still, the dampness and discipline of Sainte-Pélagie was probably more comfortable than boarding school had been. Prisoners could receive visitors every Thursday and Sunday, chat among themselves, walk about. Nevertheless, Galois soon fell into despair. Some of his co-inmates began referring to him as “an old man of twenty”. His sister Nathalie, who visited constantly, thought the same, finding him as hollow-eyed as someone 30 years older. Galois had already proven at the banquet in May that he could drink beyond his limits⁠—an ability that he now had cause to demonstrate repeatedly. Fellow inmate François-Vincent Raspail, the president of the banned Société des amis du peuple, describes how prisoners taunted Galois by calling him a water-drinker. In response, Galois began downing entire bottles of brandy in one go, with predictable consequences. His mental state deteriorated, reopening his grief over the death of his father. He may even have attempted suicide, prevented only by Raspail’s intervention.

But Galois also spent a great deal of time in prison pacing and doing mathematics in his head. He even worked out a plan to bypass the Academy and publish two manuscripts privately with the help of his friend Auguste Chevalier. One of these papers⁠—”On the Conditions for Solubility of Equations by Radicals”⁠—was a revision of the paper that the Academy had balked at; the other was a new work on “Primitive Equations Solvable by Radicals”, which Galois (now particularly adept at anything having to do with radicals) seems to have undertaken starting in the summer of 1830. Before he got out of prison, he had put considerable energy into drafting a preface to the two works. This was a five-page manifesto dripping with vitriol and heavy-handed sarcasm, along with self-congratulatory sentiments about his own independence from the Academy and “how lowly I esteem my adversaries”. Among other things, he was still stewing over his lost paper.

“I must mention how manuscripts most often end up lost in the folders of Messrs. the members of the Institute, though truly I can’t conceive of such carelessness on the part of men who have the death of Abel on their conscience.”

He snarkily outlines how he could have clogged his manuscript with useless details to make it easier to understand and appease his reviewers’ request for additional information. He witheringly suggests that the examiners in charge of testing candidates for the Polytechnique deserve to be members of the Academy, given that “they certainly have no place in posterity”. He presents himself as a martyr figure, “knowingly exposing myself to the mockery of dunces”, and even obliquely lambastes the Academy for favouring applied over pure mathematics. Clearly, prison had done nothing to temper either Galois’s simmering rage or his self-esteem⁠—nor, for that matter, his politics.

In spite of this, Galois was released from prison in March, before he had completed either his manuscripts or his sentence. The authorities sent him to a small halfway house run by a man named Denis Faultrier to recover his broken health. The transfer dramatically changed things. Back in prison, Galois had told Raspail that the one thing he truly lacked was someone he could love “with his heart alone”. Now that lack was about to be rectified⁠—but it would not end well.

After his transfer, Galois became acquainted with a woman named Stéphanie, and reacted to her rather as he had to his first encounter with mathematics. It turned out that Galois fell in love as wildly as he did everything else. Even as he went over old papers, presumably still working on his pair of manuscripts, he doodled Stéphanie’s name in the margins. On one page, he superimposed the names “Évariste” and “Stéphanie”; on another, he sketched out some rather elegant monograms combining the initials “E” and “S”. Clearly, Galois had it bad.

The object of his fixation was almost certainly Stéphanie Félicité Poterin du Motel, a cousin of Denis Faultrier’s. Nearly 20 years old, she did not seem to reciprocate Galois’s affections. On 14 May 1832, she wrote to him:

“Let us please make an end of this matter. I do not have sufficient wit to follow a correspondence of this type, but I will try to have enough to converse with you as I did before anything happened… no longer think about things that could not exist and that never will exist.”

Another excerpt was even more crushing:

“…be persuaded, Sir, it would doubtless never have been more; you are assuming wrongly and your regrets are ill-founded.”

She ruled out even the possibility of a friendship, telling Galois that he was wrong to believe that men and women could ever be true friends.

A heartbroken Galois swirled downwards into an emotional whirlpool. His friend Auguste Chevalier grew alarmed, thinking that Galois was revelling in his own misery; Chevalier accused him of “being drunk on the putrefied muck of a rotten world infecting [his] heart, [his] mind, and [his] hands.” In a consoling letter, Chevalier apparently urged him, not for the first time, to seek refuge in religion. On 25 May 1832, Galois wrote back.

“[H]ow can one destroy the traces of emotions as violent as those I have passed through? How can one console oneself for having exhausted in one month the greatest source of bliss available to man, to have exhausted it without bliss, without hope, certain one has drained it dry for life? […] for your part, you feel obliged to do your best to convert me. But it is my duty to warn you, as I’ve done a hundred times, that your efforts are in vain. […] I’m disenchanted with everything, even the love of glory.”

Still, this all-encompassing existential loathing did not stop Galois from looking forward to reuniting with Chevalier in a few days. But the trip never happened. What actually happened in the next four days is unknown, but the night of the 29th found Galois desperately dashing off additional letters instead of sleeping. One was addressed to a pair of his republican friends:

“I have been challenged [to a duel] by two patriots…it was impossible for me to refuse.”

Officially, duelling was illegal at the time, but Galois was right. Like most of the rest of Europe, plus the New World (hello Mr. Hamilton, Mr. Burr), France was in the grip of a duelling frenzy. If anything, the historical reality makes the way the Three Musketeers duel at the drop of a hankie seem downright restrained. More than 200 people died in duels in France between 1826 and 1834 alone. Alexandre Dumas knew this firsthand: he had won his first duel when he was 22 (though his trousers had fallen down in the process). Politicians blew out the brains of other politicians, journalists from opposing sides of the political divide killed each other with pistol or sword, authors and literary critics could be found on the fighting fields, young men took aim at each other over women, professional killers went around challenging people for jostling them in the street. In Bordeaux, a duelling club was founded whose members swore to only ever fight to the death: the association lasted three years, until a newcomer systematically killed all twelve surviving members. In 1837, two law professors took up swords over whether a certain passage in the 6th-century Digest of Justinian should end with a colon or a semicolon. (Professor Semicolon won by sticking three inches of steel into Professor Colon’s arm.) The poet Lamartine, who ended up in a duel in 1825 after one of his poems included a mildly uncomplimentary line about Italy, summed up the ethos by remarking that “It takes more courage to refuse one duel than to fight ten”.

In this atmosphere, there was never any question as to whether Galois would accept the challenge: any young man refusing would forever be branded a coward, and a fellow of above-average hotheadedness was unlikely to consider the possibility anyway. But Galois did not think he was fighting a duel for a particularly glorious cause. In a letter he addressed to “all republicans”, he wrote:

“I die the victim of a shameless flirt and her two dupes. My life is being extinguished in a miserable bit of gossip. Oh! Why die for something so small⁠—die for something so contemptible!”

He closed by describing himself in Latin: “Nitens lux, horrenda procella, tenebris æternis involuta”, which translates to “a brilliant light, swallowed by an awful tempest, wrapped in eternal darkness.” Id est, the turducken of melodrama.

As Samuel Johnson said, the certainty of being hanged in the morning concentrates the mind wonderfully. The possibility of being shot did precisely the same to Galois. A few days earlier, he had been doubting his ability to ever do math again; now he began a letter to Auguste Chevalier. “My dear Friend,” he wrote, “I’ve done several new things in analysis.” Then, in small, neat handwriting, over seven pages, he frantically set about getting down as many of his original ideas as he could. These provided enough material, Galois claimed, for three manuscripts. The first was the one the Academy had shrugged at; Galois insisted he stood by it, with only a small number of corrections. He then sketched out the most important parts of the other two manuscripts that he envisioned. Only at the end of the letter did some sense of finality come into play:

“You know, my dear Auguste, that these are not the only topics that I have explored […] But I don’t have time and my ideas are not yet very well developed in this immense area.”

He concluded by asking Chevalier to publish the entire text of the letter itself in the Revue encyclopédique, and to publicly ask mathematicians Carl Gustav Jacob Jacobi or Carl Friedrich Gauss, or both, “to give their opinion, not on the truth, but on the importance of these theorems”. He also defended himself against the risk of again being accused of cursory mathematical argumentation:

“In my life, I’ve often taken the risk of advancing propositions about which I wasn’t certain. But everything I’ve written here has been in my mind for almost a year, and it is too much in my interest not to make mistakes for anyone to suspect that I’ve here formulated theorems for which I don’t have complete demonstrations.”

And yet, on the night of the 29th, Galois also revisited the copy of the manuscript that the Academy had returned to him. At one point, he scrawled in a margin, “There is something to be completed in this proof. I don’t have time”⁠—a poignant admission that reviewers’ calls for greater clarity had not been entirely undue.

At the scheduled time, on the outskirts of Paris, with a handful of witnesses, Galois and his challenger chose their pistols. It is possible that only one of them was loaded⁠—an uncommon but not unknown option that added an element of Russian roulette to the mix. The two men walked to twenty-five paces, turned to face one another, and shot. Hit in the abdomen, Galois dropped to the ground. Someone⁠—possibly an onlooker, possibly a passerby⁠—transported him to the nearby Cochin Hospital.

Conscious, but badly wounded, Galois lay in a room with four or five other patients. The only family member to have heard about the duel was his younger brother Alfred, who raced to the hospital and soon became despondent. Galois’s wound was not only severe, but also oddly positioned. It was as if he had not tried to minimise his chances of being shot; he might not even have turned to the side as he faced his foe as was customary. The injury was extensive, and already infected. The hospital surgeon and both brothers all knew that there was little to be done. Alfred was in tears, but Galois stoically instructed his brother, “Don’t cry. I need all of my courage to die at the age of twenty.” He characteristically rejected an attempt to have a priest attend to him, then, at 10:00 a.m. on 31 May 1832, Évariste Galois died in his brother’s arms.

Legend has long held that a large crowd attended Galois’s funeral that Saturday. The Prefect of Police claimed much later in his memoirs that some two to three thousand people were there. However, on the day itself, the same man’s report to the Minister of the Interior stated that the actual number was around 150, mostly other republicans. They set off at 11:30 a.m. on 2 June to accompany Évariste Galois from Cochin Hospital to the Montparnasse graveyard. After some good old fiery political speeches, Galois’s body became the 18th of 21 to be placed in a common grave⁠—after which the attendees passed the hat around to pay for the funeral costs.

Perhaps more than 150 had intended to be there. Paris was (again) on the verge of insurrection, and the republicans were looking for an excuse to gather and start a riot. Galois’s funeral might have fit the bill perfectly⁠—except that the day before saw the death of General Jean Maximilien Lamarque. Lamarque was a prominent advocate for the wretched, miserable poor⁠—who, despite what certain modern stage productions suggest, were not inclined to be tuneful about their state. The republicans quickly realised that Lamarque’s funeral would be the higher-profile event, and rescheduled the rebellion. Thus, Évariste Galois was once again shoved aside and left out, even in death. His duel deprived him by just a few days of the opportunity to die a glorious republican martyr in the ill-fated 1832 June Rebellion. His friends of the Société des amis du peuple would appear thinly disguised in one of the best-selling novels of all time, but there are no mathematicians among the students in Victor Hugo’s Les Misérables. Adding insult to fatal injury, among those who fought heroically on the June barricades, and survived, was a certain Étienne-François Pecheux d’Herbenville⁠—who most likely fired the bullet that prevented Galois from ever getting to join a revolution.

The identity of Galois’s opponent has long been one of the many mysteries surrounding the duel. Alexandre Dumas specifically named him as d’Herbenville, but Dumas is not infallible, and other evidence seemed to suggest otherwise. Two days after the duel, a newspaper from the town of Lyon, Le Précurseur, reported on the duel, describing the victor as “one of [Galois’s] old friends, like him a very young man, like him a member of the Société des amis du peuple, and who had … also been a figure in a political trial”. The article attributed the duel to a romantic argument, and identified Galois’s foe by the initials “L.D.”

The Précurseur article is full of small inaccuracies, but even taking these into account, it is tricky to make their depiction match Dumas’s identification. On the one hand, d’Herbenville⁠—a charming young man who liked to wrap his cartridges in pink silk paper⁠—was indeed a republican. In fact, he was one of the nineteen republicans whose acquittal was celebrated with the notorious banquet that ended with Galois’s drunken oath and Dumas’s autodefenestration. But beyond this there was no evidence of any connection between the two, let alone of old friendship. Given that Galois did not have many friends, other candidates have been sought. Mario Livio, among others, has argued for Galois’s friend and fellow prisoner Ernest Duchâtelet, who has the advantage of both being a friend and having at least one of the right initials.

Recent discoveries, however, make it almost certain that Dumas was right after all. One key piece of evidence is a copy of France’s 1791 revolutionary constitution. Among its owners was a Swiss medical student named Larguier, who wrote on it, “This manuscript was given to me by Gallois killed in a duel by Pécheux d’Herbinville”. Meanwhile, Olivier Courcelle’s research has discovered that d’Herbenville’s names were rarely spelt the same way twice in the press. Among the variations were forms such as “Lepescheux” and “Dherbinville”⁠—these would give us the “L. D.” reported by Le Précurseur. Most tellingly of all, recent close analysis of Galois’s manuscripts has shown that, though crossed out, d’Herbenville’s name appears in Galois’s papers, proving that the two were indeed connected somehow. How, and as of when, is unknown, but Courcelle has discovered that d’Herbenville took classes at Louis-le-Grand at the same time that Galois resided at the school. Moreover, d’Herbenville studied mathematics at school before turning his attention elsewhere, and eventually became an engineer. In d’Herbenville, Galois would have found a radical republican he could talk shop with.

But knowing the identity of Galois’s killer does not solve the greater mystery of why the duel was fought at all, nor explain its oddities. The confusion over who took Galois to the hospital suggests that he went into the duel without any witnesses of his own⁠—a baffling choice given that one of the witnesses’ duties was to ensure prompt medical care for the wounded. Between this and Galois’s uncommon injury, several commentators have suggested that Galois went into the duel intending to die. One theory even holds that he was sacrificing himself for his political cause. But this is difficult to reconcile with his open letter to “all republicans”, in which he begs “my friends the patriots not to reproach me for dying for something other than the country”. Instead, he attributes the death he foresees for himself to “a miserable bit of gossip”. Moreover, one of Galois’s last-minute letters suggests that the challenger(s) “charged me on my honour not to inform any patriot” (italics in original). Galois’s devastated brother Alfred, meanwhile, thought Galois had been shot by secret police agents acting on behalf of the king. This is profoundly unlikely. Even if Louis-Philippe’s regime had been prone to assassinating people⁠—which it does not appear to have been⁠—Galois was simply not important enough to warrant eliminating, particularly in such a convoluted manner.

More likely, it was simply a ‘matter of honour’⁠—and the generally accepted explanation is that the honour in question was Stéphanie du Motel’s. Most commentators identify the ‘shameless flirt’ of Galois’s letter as Stéphanie, though whether she deserved that appellation is entirely unknowable⁠—as is whether the challengers were in any way ‘dupes’. Quite possibly, Galois had simply importuned her so much that she had no option but to ask for assistance. Certainly, Galois indicates that he insulted his challengers, and did so to their faces: he wrote in his open letter that he “repent[s] having spoken a fateful truth to men who were so poorly prepared to hear it coolly”. With Galois’s temper, it seems unlikely that any of it was done coolly. As research continues into Galois’s papers and what he crossed out where, answers may yet come to light. Recent findings have confirmed that there was a police report about the duel; perhaps it will be found in an archive somewhere.

Alfred Galois and Auguste Chevalier were left with the weighty task of doing justice to Évariste Galois’s mathematical legacy, and it took time. It was not until 1843 that Galois’s luck changed, when his work reached French mathematician (and member of the Academy) Joseph Liouville. As he worked through Galois’s papers, Liouville noted their brevity and relative opacity, but realised that what Galois had proposed years before was both mathematically rigorous and far ahead of its time. In 1846, Liouville published Galois’s “ingenious and profound” work in his own internationally renowned journal, and thus it reached the wider mathematical community at last. Within 15 years, what came to be known as Galois theory was being taught in algebra classes. Historian Amir Alexander says that Galois “had become an iconic figure of the field, a revered martyr to mathematics”.

It is a curious fact that what seems at first glance to be nothing but “pure” mathematics often later turns out to have important applied uses. While the Academy of Sciences could not see the practical side at the time, Galois’s new ways of approaching symmetries, permutations, and groups turned out to apply to, well, basically everything. Subtle symmetry appears to play a profound, central role in the laws of physics as we understand them. It applies just as well to the miniscule (particle physics) as to the humongous (cosmology), and is scattered throughout just about everything in nature that shows organised behaviour. One can only imagine what Galois might have been able to contribute with more than just a few years of research.

The story of Évariste Galois⁠—a revolutionary in every sense⁠—has become something of a legend in the last 150 years, not least because of the dual figure he presents as mathematical visionary and political lightning-rod. Early obituaries all focused on him as a republican. As early as 1846, however, Liouville could dismiss Galois’s political activities as nothing more than “a pity”, and for several decades this was the common verdict. Neither of these is the full story. Galois’s mathematical thought and his political thinking are deeply intertwined. In one of his draft papers, an equation that cannot be broken down further leads him to write the word “Indivisible”, and beneath that, “Indivisibility of the republic”, followed on a new line by “Liberty, equality, fraternity, or death”. Among the scrawls on the same page are the words “Une femme” (“a woman”)⁠—and, deeply scrawled out and now visible only with specialised equipment, the name of Pecheux d’Herbenville.

Galois closed his final mathematical statement with the bitter hope that after Jacobi and Gauss had given their opinion on the importance of his theorems, “there will be, I hope, some people who will find it to their advantage to decipher all this mess.”

There were, and they did.

© 2020 All Rights Reserved. Do not distribute or repurpose this work without written permission from the copyright holder(s).

Printed from https://www.damninteresting.com/radical-solutions/

Since you enjoyed our work enough to print it out, and read it clear to the end, would you consider donating a few dollars at https://www.damninteresting.com/donate ?