© 2006 All Rights Reserved. Do not distribute or repurpose this work without written permission from the copyright holder(s).
Printed from https://www.damninteresting.com/retired/never-say-never/
This article is marked as 'retired'. The information here may be out of date, incomplete, and/or incorrect.

Don’t you just love proving people wrong by doing what is supposed to be impossible? My own personal triumph was beating the Saltine myth – I was once told that it was impossible to eat seven Saltines in a minute, and after a few attempts, I was able to prove them wrong (as well as ensure that I’ll never want to eat a Saltine again). I then proceeded to lick my elbows and say “toy boat” ten times quickly. It’s all possible, even though many don’t believe it.
However, there’s one challenge I have never been able to figure out – how to fold a piece of paper more than eight times. I have heard it stated as fact that one cannot fold a paper in half more than eight times, because the doubled and re-doubled paper quickly becomes too thick. This reasoning had always seemed pretty odd to me – what was this magical property of hardened tree pulp that caused it to stop folding after so long? Thanks to a student named Britney Gallivan, it turns out that this impossibility is just as mythical as not being able to lick your elbows. By developing her own formulae for paper folding, she calculated how much paper one needs to achieve any number of folds (and herself managed to break world records by folding a piece of paper twelve times).
It all started Gallivan’s junior year of high school in 2001 when she was given an extra credit challenge for math – fold a piece of paper twelve times. (Don’t you love it when teachers give you extra credit for what they assume is an impossible task?) She figured that either the paper had to be quite wide, or very thin; she went with the latter for her first attempt. Using some precise tools, she was able accomplish the feat using gold foil, which is only eleven millionths of an inch thick. Of course, this was not good enough for the teacher, who insisted that something with of the thickness of paper should be used for the challenge.
Back to the drawing board, Gallivan now had to calculate how big of a sheet of paper she needed in order to fold it twelve times. First, she specified what a paper with n folds was, based upon the layers seen in the paper. One fold would have two layers, two folds would have four layers, three folds would have eight, and so on; in other words, n folds meant 2^n layers.
She also determined the equations for how much paper was needed for folding, based upon the way paper folds. She came up with equations for both alternating and single-direction folding (alternating is what some people call “hamburger-hotdog” folding, whereas single-direction keeps folding the same point over and over again).
For single-direction folding, the equation is:
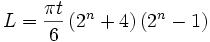
Where L is the minimum possible length of the material, t is material thickness, and n is the number of folds possible in one direction. L and t must be the same unit.
For alternate-directional folding, the equation is:
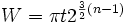
Where W is the width of a square piece of paper and n is the number of paper folds. This equation is not exact, but gives a close approximation of the limits for paper size.
If one looks at her equations and the thickness of a basic 8.5″ by 11″ paper, it makes sense that it was thought that folding a paper more than eight times would be impossible. However, instead of being impossible, it’s merely a problem that gets exponentially more difficult with each iteration. Think about the story where a king pays an artist a penny for his first day of work, two pennies on the second, and so on – by the end of a month, the artist is making more than a million dollars a day. The paper folding problem is equally distressing as the king’s future debt to the artist.

Ultimately, Gallivan discovered that for a large number of folds, single-direction folding required less paper. However, in order to achieve her teacher’s required twelve folds, Gallivan would need a 4,000 foot-long piece of paper. She eventually found a roll of special toilet paper that matched the job, and set out to break a record.
Unrolling the paper in a mall at her hometown in Pomona, California, she and her parents went to task. After seven long hours of folding their hearts out, the three successfully executed twelve folds, shattering the previous world record. For her efforts, Gallivan received her extra credit, and in the process she changed the world in an indiscernible but distinct way. As for the generations of people who have asserted that such a feat is impossible, Britney proved them wrong once and for all. It’s amazing what you can accomplish with a little imagination, a double-helping of ambition, and an industrial-sized roll of toilet paper.
Further reading:
Historical Society of Pomona Valley article on Britney Gallivan
Wolfram Mathworld on the Mathematics of Folding
© 2006 All Rights Reserved. Do not distribute or repurpose this work without written permission from the copyright holder(s).
Printed from https://www.damninteresting.com/retired/never-say-never/
Since you enjoyed our work enough to print it out, and read it clear to the end, would you consider donating a few dollars at https://www.damninteresting.com/donate ?
1st?
I was always a big fan of mundane world record holders. They have a quiet dignity about them, not like the loud mouth bragards who can “run the fastest” or “jump the highest” or whatever.
Cool article but I can’t get the pics up.
cute girl :)
…yeah, yeah, off topic, I know ;P
In college, my discrete math professor gave out 4 special problems over the course of the semester. If you could solve one of them by the next class, you would earn an automatic A for the course. I don’t know if he assumed that the problems were unsolvable in that amount of time, but I sure enjoyed my A.
There must be some bizarre satisfaction in publicly disproving myths and earning your name in the Guiness World Records, I just don’t get it. Personally I’d rather see Britney Gallivan lick her own elbows. Good article Daniel.
The challenge of folding a paper 8 times is supposed to be done on a standard 8.5′ x 11′ paper (or something similar such as A4 in some places), that is supposed to be part of the challenge…
I would not consider toilet paper an acceptable form of paper. I say she cheated…
I’d heard that about the paper size issue too.
Oh, and I can lick my elbow! Not jut touch it, but full on slobber all over my elbow if need be… but only my left elbow, even though I’m right handed. Off topic, but I’ve always wanted to tell lots of people!
how the hell do you lick your elbow?
She sure showed her teacher.
As i would say, “Owndizzleified!”
but good for her for actually making a mathematical formula! Hey! I can’t lick my elbow either. how do you do that?!
Don’t look at me, I’m not going to lick your elbow either!
Just how many points of extra credit was this worth exactly? That’s a lot of work to go through just to earn another 25 points or whatever, unless she was failing and NEEDED those 25 points.
I feel like a lazy bum having typed that. =P
Yes, as stated above, I think a standard 8.5″ x 11″ sheet of 20 lbs. paper is part of the problem. Using 4,000′ of toilet paper is kinda cheating and, I would say, a disqualifier for a world record. Hell, if I want a world record, I’ll get an 8,000′ roll of TP and fold that bastard 13 times placing me in the Guiness Book of World Records. Blah… Give me a real task once thought impossible which has been overturned.
ok, how about you end war in the middle east once and for all. Now thats a real impossible task, OR IS IT :)
Ahhh! Math at 5:30 am just ain’t right! But good for her. I don’t think it matters how much extra credit she got. What’s more important is that she took a challenge and not only found a way to solve it, but also created some new equations in the process. It may just be because I’m functionally illiterate when it comes to math, but that just impresses the dickens out of me. I’d say that this high schooler has a brilliant future ahead of her.
Oh, and one more thing for all you nay-sayers. Take a few minutes and go to http://www.youtube.com to see what most high school kids are doing these days. I think you’ll find that having someone like Britney, who actually thinks about things other than booty dancing to Gangsta Rap, or finding creative new ways to hurt themselves with skateboards or shopping carts, is a shining ray of hope for our future.
Sorry, I’m putting my soapbox away now.
Cool beans, you know ive been bored before lol, but uhhhh not quite that bored. but kudos to her for doing some major thinking outside the box.
I don’t really think she broke the record. Toilet paper is not really paper. You could say that she is thinking outside the box, but I think that when we say paper, we mean real paper. Toilet paper is more flexible and softer than real paper, so it would be easier to fold. Then again, to be fair to her, the only way she could get a piece of paper that size is by using industrial size toilet paper.
I still think the myth has not been disproved.
Your next assignment, Britney: Putting the toothpaste back in the tube.
I think its great. Hats off to Britney for ingenuity, perseverance, and spending her own time to develop it. Hey all you folks, what if this was YOUR kid? Would you still find a way to take the shine off of her acheivement? And why would I want to lick my own elbow? Isn’t that why we have dogs?
Dustin Barbour said: “Yes, as stated above, I think a standard 8.5″ x 11″ sheet of 20 lbs. paper is part of the problem. Using 4,000′ of toilet paper is kinda cheating and, I would say, a disqualifier for a world record. Hell, if I want a world record, I’ll get an 8,000′ roll of TP and fold that bastard 13 times placing me in the Guiness Book of World Records. Blah… Give me a real task once thought impossible which has been overturned.”
No one is giving Britney credit for deriving those equations, finding two (count ’em!) unique solutions, and working out the logisitics to solve this problem that’s been around for decades (centuries?). I believe she deserves all the credit she’s been given. I’m going to keep my eyes open for a Damn (un-) Interesting article about someone folding an 8000-ft sheet of paper.
http://www.straightdope.com/classics/a4_241.html
I AM CORNHOLIO!!!!!!!!!!!!!!!
dictionary.com
5 entries found for piece.
piece Audio pronunciation of “piece” ( P ) Pronunciation Key (ps)
n.
1. A thing considered as a unit or an element of a larger thing, quantity, or class; a portion: a piece of string.
I say give her one sqaure of TP and lets see her do it again.. I mean by definition it must be a element of the larger set… “A” piece..
Ironclaw said: “dictionary.com
5 entries found for piece.
piece Audio pronunciation of “piece” ( P ) Pronunciation Key (ps)
n.
1. A thing considered as a unit or an element of a larger thing, quantity, or class; a portion: a piece of string.
I say give her one sqaure of TP and lets see her do it again.. I mean by definition it must be a element of the larger set… “A” piece..”
I’d say that 4000 feet of toilet paper is definately a subset of the thousands of miles of it produced a year. Give the kid a break, people!
djsteiniii said: “No one is giving Britney credit for deriving those equations, finding two (count ’em!) unique solutions, and working out the logisitics to solve this problem that’s been around for decades (centuries?). I believe she deserves all the credit she’s been given. I’m going to keep my eyes open for a Damn (un-) Interesting article about someone folding an 8000-ft sheet of paper.”
The way I learned this – is that paper size/thickness does not matter: in maths class at high school, we were actually told just to take any paper and try to fold it more than 8 times. We tried it with a newspaper folded out, we tried it with the very thin tracing paper (or whatever you call that) – it did not work.
What I’m trying to say is that she may deserve more credit, than she’s getting from above comments – I think the principle is that when folding it, you always halve it, which after 8 folds *always* will give you a folded piece that cannot be folded any further, so size does not matter :-)
Anyways, I am not a math-genius – maybe other people more adept at formulas will comment?
Finally a really good use for tp.
All together now … eeewwww.
I like this chick alot.
Although I am not sure she’s the only one who came up with these equations…the essence of folds, flatness, and planes is not a new topic. Some cool things have been done with it. But, I can be wrong..talking off of the top of my head. I bow to the princess Britney.
Good to see that people are finding better things to do with their minds beside watch T.V. or doing drugs. People like her, those are the ones that have direction in life and amount to something. Good job Brit.
Another possible source of paper would be the paper rolls used in printing newspapers. These come in huge drum-rolls, many thousands of feet long (So huge you have to use a forklift to move them!).
Yet another source of paper would be one of the rolls of paper used in something like the IBM Infoprint 4000 (or 3900) series of printers (And, those printers are pretty DI, too.).
Dave
According to the formula, you would need a roll of toilet paper 16000 feet long to get 13 folds (not simply 8000 feet as Dustin suggested).
Use L= 4000ft, and n=12 to solve for t to determine the thickness of the toilet paper (~0.000455 ft).
Solve for L using t above and n=13 to get almost 16000 feet exactly.
And THAT is a lot of toilet paper.
Some clarification: The challenge that people thought was impossible was any peice of paper, any size. My guess is that this was born out of many attempts with a standard piece of paper; and for any size and width of paper, there is now a known limit to how many folds it can have (as given by Gallivan).
As for doing 13 folds… it’s possible, but would require quite a bit of determination! Even if you find a sheet of paper of the right size, I cannot imagine how much a pain in the ass it would be to have to travel a few miles just to make one fold in a piece of paper.
This is hooey! I can fold my underwear 17 times! Oh, and I love french toast.
OK, so here’s the key point which is not discussed above: Toilet paper is both far more compressible and far more stretchable than binder paper, printer paper, or newsprint. That’s why it can fold so many times without tearing. The interior folds compress, the exterior folds streeeetch, and the mission is accomplished.
Can someone get this girl a boyfriend? Its evident she was a little bored…and desperate for the extra credit…
gibcat said: “According to the formula, you would need a roll of toilet paper 16000 feet long to get 13 folds (not simply 8000 feet as Dustin suggested).
Use L= 4000ft, and n=12 to solve for t to determine the thickness of the toilet paper (~0.000455 ft).
Solve for L using t above and n=13 to get almost 16000 feet exactly.
And THAT is a lot of toilet paper.”
…why not turn the paper over and fold the other side? Seems simple enough.
Oh, btw…when you’re done…please tear it into smaller strips for use later on. Thank you.
Have to say it: industrial toilet paper is not perforated into little individual sheets – look carefully at the bottom pic – which qualifies it as a single “piece,” like a roll of newsprint. Technically, she did this with one piece. A little creative marterial acquisition goes a long way, huh?
And: when I was in high school I had a thing with paper – I was using rolling papers a lot, for other – psychadelic – reasons. This girl didn’t cure cancer or stop world hunger, but she whupped the establishment and went all out just to get agood grade, and that took some guff. Good for her, I say!
Marius said: “Oh, and one more thing for all you nay-sayers. Take a few minutes and go to http://www.youtube.com to see what most high school kids are doing these days. I think you’ll find that having someone like Britney, who actually thinks about things other than booty dancing to Gangsta Rap, or finding creative new ways to hurt themselves with skateboards or shopping carts, is a shining ray of hope for our future.
Sorry, I’m putting my soapbox away now.”
Why can’t she booty dance AND be an aspiring mathematical genius? As I understand it, it’s important to be well-rounded.
To add to that:
In fact, I think it’s part of the rebellion of teenager-ism that prompted her to do this. Her teacher made it clear that she didn’t think anyone could do it, and she said “screw that, yes I can” and then did.
I think my own personal disregard for overbearing authority during my teenage years made me a more creative person in adulthood.
So maybe teenagers do stuff like skateboard off the roofs of houses but it’s mostly because they’re very concious that there’s some old woman across the street going “Look at those stupid kids” and they think it’s hilarious.
dabbie said: I think the principle is that when folding it, you always halve it, which after 8 folds *always* will give you a folded piece that cannot be folded any further, so size does not matter :-)
size does matter. the longer the piece of paper is the easier it is to fold . . . say you have 3feet of toilet paper
now let’s fold it . . . 1fold 18inches 2 folds 9inches 3folds 4.5inches 4 folds 2.25 inches at this time you have so little to fold, making it very difficult. ok let’s say we fold 4,000 feet of toilet paper. . .
1fold 2,000 feet 2folds 1,0o0 feet 3folds 500 feet 4folds 250feet. At 4 folds you still have 250feet to fold instead of the 2.25 inches. . . you get what i am saying?
Oh, come on people, give the girl a pat on the back. At least she was using her brain. Doesn’t everyone at on time or another take on the impossible? Give Britany a big piece of pie with extra whipped cream. You go, girl.
What made me sit back & scratch my head is the statement on the Wolfram Mathworld link above:
Assuming it were possible to fold paper without restriction, the height of a piece of folder paper would double in thickness each time it was folded. Since one sheet of typical 20-pound paper has a thickness of about 0.1 millimeter, folding 50 times (if this were physically possible, which of course it is not) would produce a wad of height 1.13×10^(11) meters, and folding one more time would make the stack higher than the distance between the Earth and Sun.
That’s one big wad of TP. And according to my calculations using the above formula (no guarantees that they are correct, and no insult taken if you correct me) a wad folded 51 times would require a roll of toilet paper 164 sextillion, 888 quintillion, 007 quadrillion, 565 trillion, 194 billion miles long. Hokey fritz!
mensadave said: “Your next assignment, Britney: Putting the toothpaste back in the tube.”
I used to do that, when I squeeze too much toothpaste. I didn’t empty a whole tube of toothpaste and then tried to put it all back, though.
This didn’t really click with me before… but why would anyone make TOILET paper that’s the same thickness as regular paper? Who would want to USE that?
I ate 12 dry saltines in UNDER 1 minute. That blows that old wive’s tale out of the water.
I think she deserves MORE credit… the TP has a much lower tensile strenght than regular paper, and each successive fold puts more pressure on the paper on the outside of the fold. I think that the use of TP was an extra difficulty modifier.
The paper on the inside of a fold when you have 1/4 of an inch tall stack of paper doesn’t have to stretch much, but the paper on the outside of the fold has to cover 1/2 an inch minimum to accomplish the fold – that puts a lot of stress on that paper. Now go look at how thick her finished stack of paper is in the picture…
I think someone should set up a scholarship fund for her just because she has taken the effort to do something constructive and shown a lot of good initiative. I’d contribute to it. People like her need to be encouraged both for the work they have done, and because of the effect seeing her rewarded like that will have on the other students around her. The more rewards people see others getting for doing the good but difficult stuff, the more likely they will be to emulate that in their own lives. When they see drug lords and gang bangers getting rewards (money, record deals, women, etc.) they are motivated to emulate them. Let’s reinforce the good around us.
We should find this Britney and invite her to be a charter member of Damn Interesting. I bet she’d appreciate the articles and be flattered to know that most of the people on this site admire her drive.
tp is actually the same thickness as regular paper. Get a piece of industrial single ply paper and try to stretch it 5% and it will have brokeen first I would bet. Surely not 10% longer. and that amount does not effect the answer. The fact it was tp was had no difference from regular paper, other than it was available. Her first equation shows with regular paper it would have folded the same! The equations are interesting. I multiplied the thickness of regular paper times the 2,048 thickness and it is the same what according to the picture she should have. Well my guess was off about 18%. The article about her work says she found that folding in one direction took less paper than folding it two ways. Her challenge was to fold it 12 times and she found through math how to find paper to do it. The fact that she did it with gold folding in both directions shows she must have problem understood. It is interesting that she was the first to fold paper in half 9, 10, 11 or 12 times. That is busting a world record!
Gibcat brought up a good point in correcting Barbor and others that did not look at the formula. Having twice as much paper will not give another fold the problem. Looks like her equation shows it could take more than 4 times as much paper to get another fold. Looks like she showed her equation and the problem is counter intuitive, yet correct. The work does seem like a good deed.
Justin Parks said: “This didn’t really click with me before… but why would anyone make TOILET paper that’s the same thickness as regular paper? Who would want to USE that?”
Obviously, you’ve never used a bathroom in certain foreign countries (Russia, for example).
Vanya said: “Obviously, you’ve never used a bathroom in certain foreign countries (Russia, for example).”
And never used the can at the place I used to work. They put a lot of effort into finding the cheapest & worst TP on the planet, mostly to keep dirtbag employees from pilfering rolls to take home.
Also, some foreign countries I’ve visited don’t bother with TP at all. That’s what your left hand is for, and why you never, ever, EVER extend your left hand to someone.
Justin Parks said: “This didn’t really click with me before… but why would anyone make TOILET paper that’s the same thickness as regular paper? Who would want to USE that?”
Vanya said: “Obviously, you’ve never used a bathroom in certain foreign countries (Russia, for example).”
Obviously none of your grand parents told you about other uses for the Sears Roebuck catalogues while visiting the outhouse back in the days of old. Apparently back then one sheet was enough. :)
Once when I said that you couldn’t fold paper more than eight times to my Dad he said he was sure you could if you used something like toilet paper.
…Damn!
Anyway, I’m sure some drunk college student has probably done something similar to this before but never thought it worthy of recording.
Spike said: “Oh, come on people, give the girl a pat on the back. At least she was using her brain. Doesn’t everyone at on time or another take on the impossible? Give Britany a big piece of pie with extra whipped cream. You go, girl.”
I guess a pat on the butt would be inappropriate?
I am certain that *kissing* one’s own elbow is impossible if it turns out I am normal in this regard; but I can imagine someone with a slightly longer tongue would have a shot at *licking* one’s own elbow especially if that doesn’t mean the pointy part specifically. I am close, perhaps an inch away, from the pointy part in my own experiments…
Ironclaw said: “dictionary.com
5 entries found for piece.
piece Audio pronunciation of “piece” ( P ) Pronunciation Key (ps)
n.
1. A thing considered as a unit or an element of a larger thing, quantity, or class; a portion: a piece of string.
I say give her one sqaure of TP and lets see her do it again.. I mean by definition it must be a element of the larger set… “A” piece..”
You obviously have no concept of what “Industrial Toilet Paper” means. You often have a huge roll of toilet paper that is not perferated but rather is torn off at the length required by the container holding it. For that matter, even regular TP is a single piece perferated to easily tear. A roll of TP consisting of separate pieces would proove to be functunally useless. Imagine trying to stack up a bunch of pieces of TP so you could wipe your butt…
I’m quite impressed at the work she put into finding the formulas. The basic principle is obvious but finding the formula and tracking down the proper length of paper in a single piece is very impressive.
While I do think her work is very cool and commend her on her efforts, I have always thought that the thing that makes the problem difficult was not the type of paper but rather the WAY it is folded. I was told that the paper had to be first folded in one direction and next in the other direction. In other words, if you were to use an 8×10 piece of paper, you would fold it in half to create a rectangle, then fold the rectangle in half to create a square, etc. Folding in the same direction makes the problem easier because you do not have the resistance of the opposing folds. Even folding the “right” way, I think it’s possible to go more than 8 times, but you’d have to start out with a football field sized piece of paper!
4,00 feet of toilet paper. That could last a lifetime for someone.
Anyways…
I say good job to her.
I guess I’m confused here. I thought the whole point to this problem is that there are parameters and since they weren’t followed, nothing was accomplished. I could say “toy boat” 10 times slowly and carefully, but that’s not how it’s supposed to be done. And it’s obvious that the spirit of the seven folds problem in this case wasn’t followed either.
The whole point of this is to take a standard sheet of paper being of standard thickness as well as measuring 8 1/2″ x 11″ in size. You then take said piece of paper and the fold in half, turn it 90 degrees, fold in half again, turn 90 degrees, again fold it in half, and so on. No one yet has gone more the seven times and regardless of what 99% of you are saying here, neither did she.
I give this girl nothing.
She did nothing.
End of story.
The record has since been broken – and legitimately.
This girl while creative did not adhere to the spirit of the challenge. She did not fold the paper correctly, it should be turned 90 degrees at each fold then folded on itself. She did not have to refold a fold with her method – thus, the longer the paper the easier to do. If she adhered to the spirit, the toliet paper would not have worked. She should never have been in any record book – breaking that record is as simple as getting a longer piece of material (paper of any kind). All you would need is the right connection in the right factory.
My 2 cents, no refunds.
MythBusters season 5 had a segment on this very subject (well after this article was written). They even mentioned Britney in their show. They were unable to fold a standard piece of paper more than 7 times. However they were able to fold a slightly larger sheet of paper 11 times! (And by slightly I mean about 170 ft x 220 ft and they used a steam roller to flatten the fold and a fork-lift to life the paper for the last few folds because the paper was so heavy, lol)
Sheryl Crow would be SO MAD at this horrible abuse of toilet paper. =P
No, come on. The challenge is “a sheet of paper”. That’s in normal parlance and with what was at one time common sense. It refers to a normal sheet of writing, or binder, or if you’re trying to cheat, newspaper. And it won’t work within those parameters. The challenge isn’t to get a sheet of paper three acres in area, nor sheets of atomic thickness of the most malleable semi-common element on the planet. It’s a piece of paper, and no, you [b]can’t[/b] fold one more than eight times.
Still, congratulations on the Saltines thing. I’d not heard of anyone who’d done that. Well, and lived, anyway.
Indeed. The point of the problem isn’t weather or not you can fold PAPER 8+ times, but a letter/A4 sheet of standard-weight (20lb) printer paper. Newspaper is sort of cheating, but is still semi-qualified for the challenge, since it’s a piece of paper people use every day. A roll of industrial toilet paper is just not an acceptable substitute. The paper the Mythbusters used was simply too large to qualify, although it had a similar ratio to regular paper. If you have to use a forklift, a steamroller, a shopping mall, or an aircraft hangar, it’s too big. Also, she shouldn’t claim that she did it, as she folded the paper in one direction only, since it did not have the L/W ratio that “real” paper does.
So TP isn’t “a piece of paper people use every day”? Speak for yourself buddy, and maybe start eating more fibre…
While you could argue that using a larger sheet of paper was cheating (and according to the parameters of the task set by her teacher it wasn’t) I have never heard that there was any inhibition regarding the way the paper had to be folded.
In fact that would be quite silly. If the only way you are allowed to solve a problem was a way someone else had already attempted and proven unfeasible, we should have stopped researching flight after Icarus died!
However regardless of whether she broke any records or not, that girl commands my respect simply because she managed to develop those equations. I consider myself quite competent in mathematics and I could not have developped those from scratch.
I challenge all those who belittle her achievement to accomplish something comparable.
Pro.
I’ve always heard that it is physically impossible to fold a paper more than 7 or 8 times, no matter what size it is. It’s one of those urban legends that goes around.